It was a Great Moment in Tech Support. The caller asked me how he could remove a word from his WordPerfect dictionary.

It was an unusual request, but we got a lot of those. “What word do you want to remove?” I asked.

He stumbled. “Um… ‘pubic’?”

I knew immediately what had happened. ‘Pubic’ is a real word, of course, but he hadn’t meant to use it in his document, and there he’d gone and given a presentation on ‘pubic works’ and how ‘pubic libraries’ operate for the ‘pubic good’. These things can happen when you speak in pubic.

His dumb spell checker had failed him. Spell checkers have been around so long that we’re used to their limitations, and one of them was that it was insensitive to context. Well, no more. Google’s DocsBlog (via Lifehacker) has announced that it’s rolled its “do you mean” spell checker into GoogleDocs.

1. Suggestions are contextual. For example, the spell checker is now smart enough to know what you mean if you type “Icland is an icland.”
2. Contextual suggestions are made even if the misspelled word is in the dictionary. If you write “Let’s meat tomorrow morning for coffee” you’ll see a suggestion to change “meat” to “meet.”
3. Suggestions are constantly evolving. As Google crawls the web, we see new words, and if those new words become popular enough they’ll automatically be included in our spell checker—even pop culture terms, like Skrillex.

How do ordinary spell checkers work?

Spell checkers work by taking words that don’t appear in the dictionary (sometimes known as ‘out-of-vocabulary’ words, or OOV), and comparing the string to a list of known words in the dictionary. To figure out the most likely suggestion, they calculate an ‘edit distance’, or how many changes it would take to go from the malformed word to a known word.

So how do you calculate the edit distance? One easy measure is the Levenshtein distance. It’s pretty intuitive. Ask yourself: How many changes would it take to go from ‘pubic’ to ‘public’? Just one: add an ‘l’. So the edit distance is 1. But the computer calculates this using a grid. This is the cool part.

Start by putting the two words in a grid like so; one word down and the other across. Also, fill the second row and column with numbers. (This will make sense in a minute.)

Now, fill each of the inner boxes with one of three numbers, whichever is lowest:

1. The number above plus 1
2. The number to the left plus 1, or
3. The number to the upper left, plus 1 if the two letters don’t match (that’s called the “cost”), or plus 0 if the two letters do match.

For our example, ‘p’ matches ‘p’, so the smallest number would be the 0 to the upper left. No cost.

On we go, down the column. None of the other letters are a ‘p’, so the lowest number for each box would be the one just above it, plus one. Notice how the numbers keep stacking up.

We start again at the next column. The ‘p’ and the ‘u’ aren’t a match, so we give it a 0 + 1 from the left, but the ‘u’ and the ‘u’ are a match, so that box gets a cost-free ‘0’ from the upper-left.

You can work out the rest of the table if you’re keen, but here it is in full.

Notice how everything’s going smoothly until the number in green, where the first real mismatch is. But the number to watch out for is that last one in the lower right, in red. When the whole table is filled out, that’s where your answer is. So the words ‘pubic’ and ‘public’ have a Levenshtein distance of 1, which matches our intuition about the number of changes we’d have to make to go from one to the other.

You can try this with any two words, either on paper, or using this handy website here. Having a play with it is a good way of getting a grip on this algorithm.

There are lots of ways we can tweak this spell-checker. We can adjust the cost so that near keys (and therefore more plausible typing mistakes) cost less than farther-away keys. We could adjust for frequency so that more common words float to the top of our suggestion list. But what we can’t do is look at nearby words to see what’s likely. That means the classic ‘form/from’ problem is beyond the reach of our spell checker.

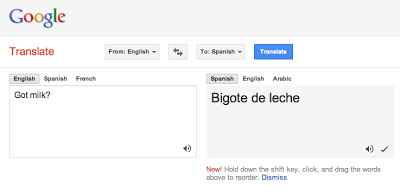
But not the one from GoogleDocs. It will flag words, even if they’re real words. Behold:

Note how throwing in a related word (‘pelvis’) in that last example is enough to calm the spell checker down.

How does it do it? It looks like it works by calculating the probability of other words appearing nearby. Articles like ‘the’ and ‘a’ are likely to appear before ‘island’, less likely before ‘Iceland’. The whole thing could be modelled with n-grams (nearby words) using a sufficiently large language corpus, which Google certainly has. And that huge corpus ensures that lots of words will be in the dictionary, including low-frequency or brand new terms.

It’s good to know that people are still adding to a technology that’s so seemingly mundane.

Back in the 1600s, people used auxiliary ‘be‘ + some verbs of motion, where today we’d use ‘have‘.

Shakespeare did it with ‘is fled‘.

LENNOX
‘Tis two or three, my lord, that bring you word
Macduff is fled to England.

And ‘is come‘.

LUCILIUS
He is at hand; and Pindarus is come
To do you salutation from his master.

I thought it would be fun to check it in Google Books Ngram Viewer, and see when ‘has X-en’ became more popular than ‘is X-en’. But you can’t do it with any old verb like ‘make’ — it has to be intransitive. Otherwise, you’re scooping up ‘is made’ constructions like ‘That’s how rubber is made.” Those are still okay now. I want the ones where ‘is X-en’ has been replaced by ‘has X-en’. And the pattern seems particularly common with verbs of motion.

Here’s ‘fled‘. Notice that the crossover happens around 1830ish.

And ‘come‘. They cross over at about the same time: 1840ish.

‘Arrive‘ arrives early — about 1810ish

Here’s ‘depart‘, right on the button — 1830 again.

And we see more or less the same pattern with other verbs like land, and become.

What was happening in English in 1800–1840?

When I raised this to the attention of fellow linguist Mark Ellison, he suggested twiddling the ‘Corpus’ menu between ‘British’ and ‘American’. This revealed that the stodgy conservative British books held onto the old usage longer. Perhaps the Americans were at the head of this ‘is – has’ innovation, and the rise we see in the corpus was partially due to more books being published in the Colonies.

I’ll have to do some looking around to see if anyone knows more about it. Luckily, I have two experts on present perfect in my very own department. Meanwhile, I think it’s cool that I can search centuries of language patterns in seconds.

Here’s an interesting application for Natural Language Processing. How do you know if a review for a hotel or a business is real, or just a spammy one written by someone who’s never even seen the place?

Computers can do it. Just get people to write a ton of spammy reviews, then get some reviews that (you suspect) are real, and compare the patterns.

Can’t read the text? Fake reviews were more likely to use “I” and “me”, adverbs like “really”, and explanation points.

Here’s a PDF of the authors’ ACL presentation.